Приведение формул обращения томографической реконструкции в конусе лучей к виду, позволяющему строить численные алгоритмы.

= g+ (x , l ) =

= gr(2 ½ S(l )½ (s2(l )x 1 v s1(l )x 2) /, - 2½ S(l )½ 2x 3 /,l ),

если < 0,

= 0, если ³ 0.

При переходе от функции g+ (x , l ) = к функции gr (P, S) интегрирование по окружности S(l ) в трехмерном пространстве заменяется на интегрирование по прямым линиям в плоскости регистрации. Отметим, что формулы обращения лучевого преобразования, использующие интегрирование вдоль прямых в плоскости регистрации.

4.3 Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования

Обобщенная функция это непрерывный линейный функционал на пространстве К всех функций a (x), имеющих производные всех порядков и финитный носитель (свой для каждой из функций α (x)). Любая регулярная интегрируемая функция f(x) задает линейный функционал (f, a ):

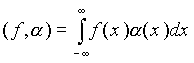. (2.2.1)

Однако на пространстве функций K существуют непрерывные линейные функционалы, которые не могут быть заданы с помощью регулярных интегрируемых функций, наиболее известными примерами таких функционалов являются δ-функция и ее производные. Другим широко известным примером является функционал, основанный на функции (1/x)dx. Функция 1/x x является регулярной, однако она не является интегрируемой. При задании соответствующего функционала интеграл

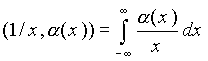(2.2.2)

понимается в смысле главного значения:

.

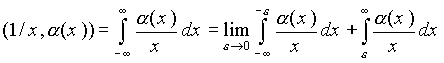Такое понимание интеграла используется при определении преобразования Гильберта от функции α (x) как свертки с функцией 1/xx.

.

Преобразование Гильберта используется, в частности, в одной из формул обращения преобразования Радона в двумерном пространстве. Эта формула обычно приводится в руководствах по компьютерной рентгеновской томографии. Однако метод свертки и обратного проецирования, часто используемый при построении численных алгоритмов томографической реконструкции, основан на несколько другом виде формулы обращения преобразования Радона. В этом методе по существу используется свертка проекционных данных последовательностью функций сходящихся к 1/xx2 в смысле обобщенных функций.

Линейный функционал, соответствующий функции 1/xx2, или, что то же самое, обобщенная функция 1/xx2 определяется формулой [19]

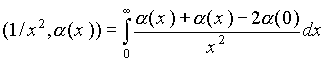(2.2.3)

Интеграл в (2.2.3) сходится в обычном смысле для любой функции a (x) из пространства основных, и даже из более широкого класса, функций.

В формулах обращения преобразования Радона используется свертка данных с функцией 1/xx2. Свертка обобщенных функций определяется следующим образом.

Пусть заданы два функционала f и g . Действие функционала f *g являющегося их сверткой, на функцию a из пространства основных задается формулой

(f *g, a )= (fx, gy, a (x + y))). (2.2.4)

Здесь gy означает, что функционал действует на функцию a , как функцию переменной y, а функционал f действует на полученную функцию переменной x. Если функционалы f и g можно задать регулярными функциям, то функционал свертки определенный формулой (2.2.4) можно задать функцией, являющейся сверткой соответствующих функций в обычном смысле.

Здесь следует сделать одно замечание. Даже если функция одной переменной a (t ) имеет финитный носитель, функция двух переменных a (x + y) не является функцией с финитным носителем. Это означает, что существование функционала f *g для конкретных функционалов f и g или необходимо доказывать. Известно, что для существования функционала свертки, достаточно, чтобы один из функционалов имел финитный носитель.

Узнайте больше ...

Современные методы лечения псориаза у детей
На сегодня проблема лечения псориаза является одной из самых актуальных в дерматологии, несмотря на то, что практически все фармацевтические лаборатории мира постоянно разрабатывают и внедряют новые препараты для лечения этого недуга. Псориаз, или чешуйчатый лишай - это одно из наиболее распространенных хронических заболеваний кожи, при котором также поражаются ...