Приведение формул обращения томографической реконструкции в конусе лучей к виду, позволяющему строить численные алгоритмы.

.

Интегрируя сначала при фиксированном p по плоскости l 1x1 + l 2x2 + l 3x3 = p, а затем по p приходим к хорошо известному выражению, связывающему преобразования Фурье и Радона

. (2.3.1)

Соотношение между преобразованием Радона и преобразованием Фурье лучевых данных.

В [21] предложен способ инвертирования лучевого преобразования, основанный на том, что по исходным данным восстанавливается преобразование Радона функции f(x)

,

что позволяет по известным формулам восстановить f(x).

При выводе формул обращения в работе используется функция

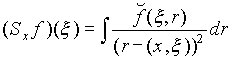. (2.3.2)

Можно показать что для функций и справедливо соотношение

, (2.3.3)

здесь С v некоторая константа. Равенства (2.3.2) и (2.3.3) дают связь между преобразованием Радона и лучевым преобразованием в трехмерном пространстве:

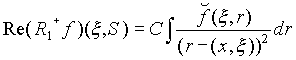, (2.3.4)

Отметим также, что поскольку

, . Равенство (2.3.4) может быть записано в виде . Из последнего равенства и определения функции следует, что функция x постоянна на плоскостях, ортогональных вектору x , так как для всех x, принадлежащих такой плоскости, скалярное произведение (x, x ) равно константе. Этот факт лежит в основе многих методов обращения лучевого преобразования. Это утверждение получено в [40], для случая комплексных пространств. Для действительных пространств это утверждение содержится в работах. Оно и может быть использовано для восстановления функции в точках x, принадлежащих области D, по значениям на ее границах.

Соотношение между преобразованием Фурье лучевых данных и преобразованием Фурье искомой функции f(x).

В работе получено равенство:

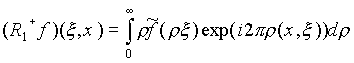, (2.3.5)

устанавливающее связь между преобразованием Фурье лучевых данных и преобразованием Фурье самой функции f, преобразование Фурье понимается в смысле обобщенных функций. Для того, чтобы использовать эту формулу для нахождения функции f нужно иметь формулы для вычисления обобщенного преобразования Фурье по лучевым данным. Такие формулы были приведены выше.

В заключение, хотелось бы сказать, что раскрытие того множества вопросов, затронутых в данной работе, можно бы было продолжать ещё очень долго, так что ряд тем представлены несколько ужато. Особый интерес представляло изучение именно технической (физической, если угодно) стороны компьютерной томографии, как метода диагностики. Замечаний к работе может, в принципе, возникнуть много, однако надеюсь на несколько снисходительное отношение – сроки были сжатые, вопрос – обширный (да и сам процесс написания прерывался - пошуровал в компьютере win95.cih).

Узнайте больше ...

Сравнительная характеристика методов лабораторной диагностики трихомоноза
Трихомоноз является одним из наиболее распространённых заболеваний мочеполового тракта и занимает первое место среди болезней, передаваемых половым путём. Инфекция имеет «космополитический» характер, от неё страдают 170 миллионов человек на земном шаре. Это широко распространённое паразитарное заболевание, вызываемое Trichomona ...